Introduction
In general, there seem to be different ways in which human beings cognitively handle sources of information. Tasks, such as number guessing, velocity, weight, and extension estimation, can be accomplished through different cognitive strategies – e.g. by counting, or comparing objects’ characteristics, and so on. In most cases, these different ways imply different performances and costs to the subject. In this paper, I offer an interpretation of these “different ways” in terms of different channel codes through which the environmental information is processed by the Central Nervous System (CNS). By considering the channel code’s cost and performance, I will distinguish among three categories of codes; prompt processing, working memory, and symbolic coding scheme. The code metaphor affords alluring explanations to important questions, such as: Why do we have the internal representation that we have – in terms of colors, extension, and texture? Why are simple theories considered better than complex ones? Why do different representations of a given system, even if conflicting, result in the same action plans (experiments)? In most cases, examples will be given through the number guessing experiments, though the general principles seem to be applicable to cognitive tasks broadly.
From the philosophical point of view, the problem of giving a suitable characterization of the role played by symbolic language in our relation with the environment has mostly taken a representationalist format. Philosophers have broadly tried to justify the successful employment of mathematical language in science through notions as ‘reference’, ‘correspondence’, ‘truth’; all of which seem to suppose a representing relation between symbolic language, on the one hand, and the world (or a model of it) endowed of predefined properties, on the other hand. The problem is that this representationalist account seems to provide no satisfactory explanation of the connection between the organism’s representations and its interactions with environment, which is the main organism’s purpose.1,2,3,4,5,6 From the psychological point of view, the idea of interpreting the symbolic language as a code is not entirely new. Dehaene in 1992, for example, has proposed a model in which different numerical representations are viewed as different processing codes for numerical magnitudes.7 However, the Dehaene’s triple-code model provides no clear indication of which mathematical tools should we employ to make this notion of code more precise. Therefore, the twofold aim of this paper is, first, to provide a characterization of the role played by symbolic language in our relation with the environment that can be connected with motor interaction. And, second, to suggest a mathematical formalist in which the code’s intuition can be suitable formulated and explored, conducting to more refined models. As a surplus, answers to old philosophical questions seem to emerge.
Theoretical framework
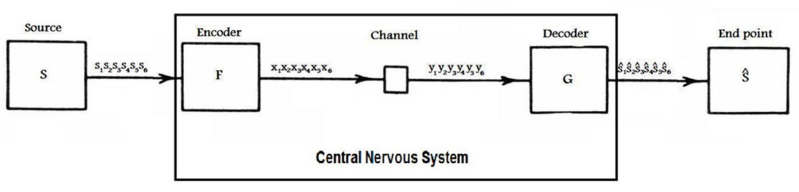
The information processing carried out by the Central Nervous System (CNS) is interpreted as the communication system whose performance is measured in terms of control. Therefore, environmental information is processed by the sensorial organs resulting in action plans whose objectives are to keep the organism alive. Whenever an accident occurs I will assume some bit of information had been wrongly decoded – the average over the suffered accidents gives the degree of control – or the lack of control. According to this interpretation, an information processing system is specified by six entities, grouped into three pairs: The source (p(s), d), consisting of a probability distribution p(s) and a distortion function d; the channel (p(y│x), ρ), consisting of a conditional probability distribution p(y│x) and a cost function ρ; and the code (F,G),, consisting of the encoder F and the decoder G functions (Figure 1). For the purpose of this paper, I will be concerned with discrete and finite alphabets.
Figure 1: Information system.
Definition 1.1 (Source): A discrete-time memory less source (p(s), d) is specified by a probability distribution p(s) on an alphabet S and a set of Hamming-like distortion functions. Let’s take the power set P(S), so that P(S)={S̿1,…,S̿i,…,S̿2|S|}. Now let us define a set of Hamming-like distortion functions
U= {d1 (S, Ŝ ),…,di (S, Ŝ ),…,d2|S|(S, Ŝ )} so that
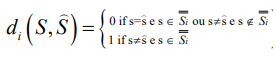 1.1.
1.1.
is called the Accident Distortion Measure, which results in a probability of error, since Edi(S,Ŝ)=Pri(S≠Ŝ). This implicitly specifies an alphabet Ŝ in which the source is reconstructed. As the alphabets are discrete, we call this, a discrete memoryless source, and the probability distribution becomes a probability mass function (pmf ).
Intuitively, the source p(s) should be interpreted as one’s environment and the 2S distortion functions as the relevant information to successful interactions in all different situations.
Definition 1.2 (Learning Function): To choose among the 2|S| distortion functions di(S,Ŝ), a set of sequences is generated according to the distribution of probability p(s), the so-called typical set of S. Then we define an index function L so that
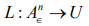 1.2.
1.2.
is called Learning Function. The learning process is a question of finding out the Learning Function L. The sequences incan be interpreted as the typical situations occurring in our world.
Intuitively, each sequence siSn should be interpreted as a typical environmental situation – i.e. the rocks falling down, hot air coming up, birds flying, fishes swimming and not otherwise – and the Learning Function as the skill of paying attention to the right things in every situation.
Definition 1.3 (Channel): A discrete-time memoryless channel (p(y│x),ρ) is specified by a conditional probability distribution, p(y│x), defined on two discrete alphabets X and Y and a nonnegative function
ρ:X→R+ 1.3.
called the channel input cost function. When the alphabets are discrete, we call this a discrete memoryless channel.
Intuitively, the notion of channel should be interpreted as the relation between perception and action and the cost function as a measure of the processing costs.
Definition 1.4 (Source-Channel Code): A source-channel code
(F, G) of rate R is specified by an encoding function
F:S→Xn, 1.4.
yielding code words xn(1),xn(2),…,xn(2nR), the set of code words is called the codebook or coding scheme.
And a decoding function
G:Yn→Ŝ, 1.5.
such that k/n = R, where n is for n uses of channel and k is for number of bits per source symbol.
Intuitively, S is the source information that affects the organism through stimuli generating an internal representation Xn. The internal representation is processed generating an action plan Yn, which is decoded as real actions Ŝ.
For a fixed source (p(s),d), a fixed channel (p(y│x),ρ), and a fixed code (F, G), we can then easily determine the average incurred distortion,
Di  Edi(Sk,Ŝk) 1.6.
Edi(Sk,Ŝk) 1.6.
and the average required cost,
Γ Eρ(Xm) 1.7.
Eρ(Xm) 1.7.
The information source S is merged in a codebook (n,2nR) through the encode function F and transmitted through the channel p(y│x) at a cost Γ. The channel output is decoded through the function G resulting in source estimation (or representation) Ŝ, resulting in a distortion D. The maximum quantity of information transmitted through the channel, given the cost constraint Γ, is defined in terms of Mutual Information as following:
Definition 1.5 (Capacity-Cost Function): The capacity-cost function of the channel (p(y│x),ρ) is defined as
C(Γ)=maxp(x):Eρ(x)≤Γ I(X;Y) 1.8.
The cost measure limits the quantity of information that the channel can transmit reliably. According to the Source-Channel Separation Theorem, if H(S)≤C(Γ), then there exist a source-channel code so that the probability of error goes asymptotically to zero. Otherwise, if H(S)>C(Γ), then the probability of error is bounded above zero – which means that the D>0.8,9 In other words, if the source entropy is greater than the channel-cost capacity, then no compression can be carried out lossless.
Intuitively, it means that when given interaction demands more information from the environment than the CNS is able to process, the probability of an accident to occur is increased. The function which gives the compression rate, for fixed distortion value D, is the Rate-distortion function.
Definition 1.6 (Rate-Distortion Function): The rate-distortion function of the source (p(s),d) is defined as
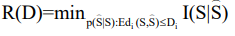 1.9.
1.9.
On the other hand, the function which gives the distortion value, for a fixed rate R, is the Distortion-rate function.
Definition 1.7 (Distortion-Rate Function): The distortion-rate function of the source (p(s),d) is defined as
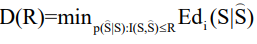 1.10.
1.10.
We are most interested in the distortion-rate function, where the parameter R=C(Γ); i.e. given the channel-cost capacity, we are interested in codes which can reduce the distortion value D as close as possible to its limit. The main objective of this paper is to compare different coding schemes and their respective distortion values Di in order to measure their efficiencies.
Prompt Processing Scheme: Subitizing
Prompt information processing is represented by the following setup: An information source S emits a sequence s1,..,si,…,sm, of bits of information, which is compressed through a encoding function F onto a channel input sequence x1,…, xi,…,xn of bits of information, for iT and m>n . The m-bits sequence is the perceptual information consisting of size, color, texture, length, numerousness, and so on, and the n-bits channel input sequence consists of our internal representations about the outside world. The clause that m>n means exactly that the coding function is lossy compressing the environmental information into the internal representation. The n-bits channel input sequence is processed through the channel p(y|x) generating an output sequence y1,…,yi,…,yn,, which is the semantic meaning invoked by the internal representation. The output sequence generated by the channel is decoded through decoding function G in a motor plan, ŝ1,…,ŝi,…,ŝk for k≤m (Figure 1). The pair (F, G)p is precisely our ordinary representations which ground our intuitive notion of reality. The channel has a cost limit Γ so that sequences x1,…,xi,…,xn have their length constrained – supposing that we’re just interested in cases of reliable transmission.
In order to measure the average of error of the code (F, G)p some psychological experimentation is needed. Some cognitive experiments assume the following general format: A perceptual sample is showed for a short period of time – often less than one second – and then it’s asked for the subject to give the suitable motor answer for it – which is either voicing something or pushing a lever or executing more elaborate action plans. An example is the guessing experiments in which a given setup is quickly shown – e.g. a set of objects – and the individual has to guess the exact characteristics of the setup. Typically, the experiments’ results present inconsiderable error average relative to sparse sources of stimuli – whether numerosity, extension, or velocity. But, as the source information rate is increased above a given quantity, the average of error starts to increase almost-linearly along with the source information rate. Sometimes this average of error is also expressed in terms of the Weber’s Fraction, which is a constant describing of the slop of variance’s growth recta related to the increasing of the quantity of information[1] – as the variance increases the error average does as well. The Weber’s Fraction, for numerical processing is around 12%,10 for size-constancy processing it is around 4%, and for the object’s speed and trajectory processing it is between 5%-10%.11 Still other perception’s modalities, such as color hues,12,13,14,15,16,17 show the same trade-off between the source information rate and error average.
The trade-off between the source information rate and the average of error can be appreciated in the number processing case. In the number guessing experiment, a setup containing a given number of entities is shown for a short period of time – often less than one second – and the subject has to guess the setup’s numerosity. The subject’s test performance gives rise to two numerical processing phenomena; subitize and estimation. In the former condition, one is able to subtly recognize the set’s numerosity up to around 3 or 4 elements while, in the latter condition, only an estimation is possible.18,19,40 As the term “subitizing” suggests, it occurs when the individual subtly recognizes the set’s numerosity as rapid as 40-100ms/item, effortless, and very accurate – practically error-free. On the other hand, for setup’s numerosity greater than 4 only estimations with some degree of uncertainty are possible, which means that the average of error is bounded above zero.
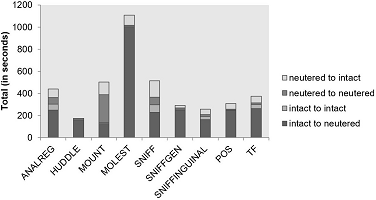
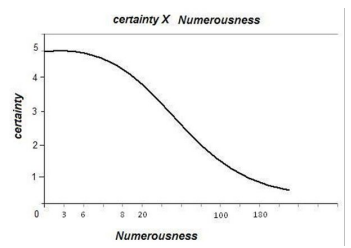
Kaufman et al represented the subjects’ number guessing performance through the trade-off between uncertainty and the source information rate (Graphic 1).18 The certainty axis is divided in 6 degrees, where 5 means complete certainty and 0 means complete uncertainty. Notice, that at 4 or 5 objects, there is almost complete certainty while it brusquely decreases after 6 objects. Graphic 1 shows clearly the almost linearly increasing of the average of error, after a given value, along with the source information rate increasing. Therefore, if few objects compose the setup, the visual representation achieves the right magnitude with high certainty; i.e. Di≈0. Otherwise, for large setup’s numerosity, the average of error is bounded above zero, Di>0. In summary, the code (F, G)p compresses the m-bits perceptual sequence in an n-bits channel input sequence, which consists of our internal representations about the outside world. As the channel-cost capacity limits the number of bits reliably transmitted, the perceptual sequence’s bits are lossy compressed in the channel input code words. The compression carried out by the code (F, G)p is a kind of all-purpose one, for even in the situations in which only numerosity is interesting, color information, for example, cannot be stripped out from the representations. For this reason, the perceptual sequence’s bits interact with each other so that a setup with exceeding color information disrupts the number processing, for example.18 The uninteresting information is called redundancy and the prompt processing scheme doesn’t seem to be a good code to handle specific situations. But why has nature endowed us with such a code? The reason seems to be that the (F, G)p code is a good code, on average, over many different situations. When the average distortion D is calculated for whole set U of Hamming-like distortion functions, di(S,Ŝ), the expected value results in a tolerable value – i.e. it keeps the organism alive in most cases.
Graphic 1: Certainty versus numerousness.
Footnote
a.[1]The guessing performance’s uncertainty can be conceptualized through different notions; for example, either in terms of variance, or entropy, or simply as a conditional distribution
Working Memory Scheme: Biological Recoding
The main idea of the previous discussion was that the prompt coding scheme is a good one when handling a variety of situations, but it is not an optimal code when handling specific tasks – i.e. it is a good source-channel code averaging over all Hamming-like distortion measures di(S, Ŝ ), but it is a bad one for a subset of them. For specific situations, where just some specific bits are relevant, a different coding function would be better.
This time I will examine how the working memory’s role in cognitive tasks fits into our previous theoretical model. The working memory is basically a memory system needed for executing complex motor tasks when the essential cues are not present in the environment at the time of the response.20 The system, in different ways, seems to help the performance of cognitive tasks. I will interpret the working memory as an encoder which employs different codes (F, G)w according to different distortion measures di(S, Ŝ).
The term ‘working memory’ refers to a brain system that provides temporary storage and manipulation of the information necessary for such complex cognitive tasks as language compression, learning, problem solving, and action planning.21 The working memory has two broad functional characteristics; maintenance and manipulation of information. According to the multicomponent model,22,23 the information maintenance is putatively carried out by three distinct systems; the phonological loop, the visuospatial sketchpad, and the episodic buffer. The first two are modal subsystems, respectively, for auditory and visual information, while the last is a multimodal integration subsystem. Still each maintenance system has two functional distinctions; the passive storage and active rehearsal of information. The passive storage retains the information temporarily and it is subject to loss by decay or interference over time. The active rehearsal of information tries to simulate the retained information so as to keep it in mind – e.g. rehearsal would correspond to the common strategy of sub vocally repeating the sequence of digits to oneself. The other broad functional characteristic, manipulation of information, corresponds to the central executive, which is responsible for recoding the information in a new format – such as when one sub vocally repeats some sequence of digits according to a specific format. Neurological evidence suggests that the anterior regions of the cortex – such as inferior frontal cortex (BA 44; Broca’s area) and premotor cortex (BA 6) – are responsible for rehearsal and manipulation, while posterior regions of the cortex are responsible for storage – such as inferior and superior parietal cortex (BA7/40) and right inferior parietal cortex (BA 40).24,25,26,27,28
Even if the temporary storage and manipulation roles can help in cognitive tasks separately, we will focus on the cases in which they seem to work together in order to recode the perceptual information.20,22,23,29 The preprocessed information is retained in one of the storage systems and then it is recoded by the manipulation system. For example, for the case in which one is interested in the setup’s numerosity, the subject can recode the setup’s numerosity in terms of “chunks” so as to surmount the prompt processing limit.30,31,32,33,34 Therefore, if the processing of numerousness was limited to around 3 or 4 objects (subitizing), then by using working memory one is able to increase this number to around 7, with very low average of error (Graphic 2) – without counting! The encoder’s role is viewed as an endeavor to deploy different source-channel codes (F, G)w in order to reduce distortion value Di according to every specific i – remember that the index i is given by typical sequence (situation) occurring. The new mental representation (channel input) generated by the working memory is very poor concerning color, size or texture information, but it is much more informative about numerical information – it is a better code for handling redundancy.
Graphic 2: Certainty versus numerousness by using working memory
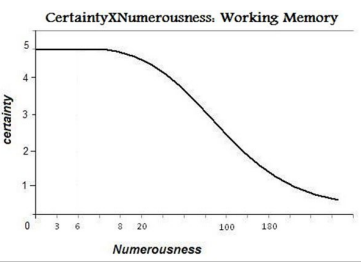
If it is plausible to interpret the working memory as an encoder, then the information kept in it should be of a preprocessed kind. Neuropsychological evidence offers support for the independence between the working memory’s information and the semantic content currently retrieved through it. Among this evidence is the fact that similarities in semantic content currently retrieved through a set of stimuli are irrelevant for the acuity with which these stimuli are kept in working memory. For example, if one were given a list of words, such as “map” “tap” “lap” “flat” and so on, it would be difficult to remember all those words because the stimuli displays similar pattern. On the other hand, if one were given a list of words, such as “house” “home” “abode” “apartment” someone would not have as much of a problem remembering even if the semantic content is about the same. This is because working memory functions at a preprocessed level not taking into consideration the semantic content.35 Still, the concurrent modal information tends to disrupt different modal information kept in working memory. There is a reduction in recalling lists of visually presented items brought about by the presence of irrelevant spoken material. The spoken material’s semantic content is completely irrelevant, with unfamiliar languages or noisy sounds being just as disruptive as meaningful words in one’s own language. These results are interpreted under the assumption that disruptive spoken material gains obligatory access to working memory.36
Even if the working memory allows the brain to surmount its limits of prompt processing, it doesn’t get far enough. This system appears to be strikingly limited in capacity, and can only store a small amount of information for short periods of time – it’s around three items for not more than three seconds–in the number processing case.30,31,32,33,34 On the other hand, working memory’s representation is still structured with the same prompt processing code’s properties – i.e. even if it privileges some kind of information, say numerosity, it cannot preclude the other kind of information, such as colors, forms, and so on. For example, if a dense colorful setup is presented, it causes the numerical capacity of visuospatial sketchpad, which is generally estimated to be about 4 items, to decrease.30,34 These results generalize the working memory’s limits for the setup’s complexity, rather than for just the number of objects.35
The Cultural Strategy: The Employment of Symbols
The working memory, as previously mentioned, is an encoding system which stores information and recodes it. The problem with this system is that it is severely limited in storage capacity. Additionally, the working memory code is too costly for optimally handling large amounts of information; its overload causes severe disruption to many cognitive tasks. A new and less costly format is the channel code (F, G)S,[1] which represents symbolic language as another coding scheme. The symbolic language coding scheme has at least two advantages in comparison with the internal representation schemes. First, it is a cheaper and more efficient channel code than the internal representation schemes and, second, it liberates the working memory to help in learning, problem solving, and planning tasks. By using a more efficient code, much more information can be reliably transmitted, which ends up improving drastically the system’s control upon the environment.
Footnote
a. [1]A similar interpretation, in terms of two mental calculation systems, has been offered by Dehaene.37
Efficiency and cost: The three-object prompt processing limit can be interpreted as the channel-cost capacity. An efficient channel code should achieve the smaller error rate by compressing the source information in code words that don’t exceed the complexity expressed by that setup. To compare two codes’ efficiency one should pay attention to its average of error on the cognitive tasks. By comparing the internal representation codes’ performance with the symbolic performance in numerical tasks, one can see the huge difference in efficiency (Graphic 3).
Graphic 3: Certainty versus numerousness by using symbolic language.
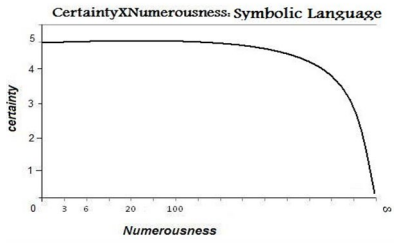
The graphic is, to some extent, speculative because mathematical skills based on symbolic language mastery vary according to cultural factors such as training, educational system efficiency, and so on. At least two groups of evidence support the interpretation of the symbolic language as a channel coding scheme; (i) the symbolic language deficit increases the error rate in retrieving the right numerical magnitude; and (ii) the symbolic systems’ evolution proceeds seems to be constrained by brain processing cost-capacity.
(i) The symbolic language deficit increases the error rate in retrieving the right numerical magnitude. There is a correlation between the bloom of the mathematical skills and mathematical language competence. The burst of conceptual and interactive mathematical skills with which to handle quantities beyond the subitizing’s and working memory’s numerical capacity is concomitant with the numerical language acquisition. The ability to count and handle larger numerosities rises in children around years old just when numerical linguistic devices start being mastered. On the other hand, evidence from Amazonian Indigene groups have supported the thesis that language is a condition of possibility for exact representation of numerosities beyond subitizing quantities. The group’s individuals, whose language misses linguistic devices for quantities larger than 3-or-4 objects, have shown only an ability to estimate over larger quantities. Neuropsychologists have found that disorders in number representation frequently are accompanied by disorders in language. Patients with brain damage in areas typically associated with language faculties have shown a severe impairment with exact numerical processing of larger quantities. These same patients, however, still keep their capacity to exactly represent quantities up to three objects and to estimate over larger quantities.37
(ii) The symbolic systems’ evolution proceeds seem to be constrained by brain processing cost-capacity. As human interaction routines require the processing of larger quantities, it increases the demand for channel code bits. Different numerical notional systems have different costs, which eventually obligate us to change from one numerical notational system to another according to the increase of the demand. The complexity expressed by the around-three-objects representation can be interpreted as standing for the channel-cost capacity limit, which doesn’t mean that this limit is the around-three-objects numerosity, as it contains figurative information as well.
Probably, the first numerical notational system used consisted of bundles of sticks paired one-to-one with the setup’s objects (Figure 2). It was the least efficient numerical notation, because its only advantage was that of keeping the informational content out of the ever changing environment, which saves short or long-term memory demand. However, as the number of sticks increases along with the set of objects’ numerosity the bundle-of-sticks coding scheme meets the same subitizing’s and working memory’s limits. Therefore, the bundle-of-sticks numerical system is a costly channel code to process quantities larger than fifteen or twenty objects. Looking at the code’s redundancy is another way to assess the code’s efficiency. Notice that every stick can be permutated without changing the code’s information, which means that the code uses much more bits than necessary to encode a given amount of information.
Figure 2: Bunch-of-sticks number system.

The second, the naming-summation numerical system is a channel code category under which, for example, are the Egyptian and Roman number systems, characterized by the employment of naming quantities and summation strategies. The notational marks are for numerical magnitudes and their repetition means their summation.38 The marks retrieve numerical facts stored in long-term memory whose meaning is provided by inborn numerical skills or constructed by combining them. For example, the Egyptian inscription of the number 543 is HHHHHTTTTUUU, where the symbols H, T, and U denote the powers 100, 10, and 1, respectively. Through the use of the naming-summation numerical system the numerical information can be compressed in shorter code words than those provided by the bundle-of-sticks system (which is coextensive with the subitizing’s and working memory’s limits) – the Roman numerical system, which uses subtraction notations as well, produces even shorter compressions. However, as the permutation test indicates, the representation provided by the naming-summation numerical systems still contains too much redundancy; e.g. the code words HHHHHTTTTUUU and HHUHUHTTUHTT express the same numerical quantity. Even though the naming-summation numerical system permits us to process exact quantities in the hundred’s magnitude, it becomes too costly to process numerosities around the thousand’s magnitude, meeting the subitizing’s and working memory’s limits.
The third example is the multiplicative numerical system – e.g. Chinese number system.38 The multiplicative numerical system is also based on underlying additive and naming principles, but a supplementary multiplicative principle allows for suppression of the cumbersome repetitions of the symbols belonging to the same rank. Different symbols for each unity (u1,u2,…,u3) are introduced. The Chinese 543 is therefore written in the form, u5Hu4Tu3. Although the multiplicative system uses five different symbols instead of three needed in hieroglyphic Egyptian, it makes it possible to compress the numerical information in shorter code words. However, as some permutation is still permitted – u5Hu4Tu3 means the same as – u4Tu5Hu3 the representation provided by this category of notation contains redundancy.
The last numerical system is the positional numerical system – the Arabic Number System.38 This system was developed some time in the first half of the sixth century A.D. in India, from whence it spread more or less rapidly to the whole world through the Arabic people. The system uses only 10 symbols, the same former system’s operations, and the rank of the units abstractly symbolized by the position occupied by these units in the code word. The Arabic numerical system encodes quantities in the usual way, as we know it, and produces very short compressions of huge quantities – e.g. 1080 , which is approximately the number of atoms in the entire observable universe. It also provides us with powerful algorithms by which different quantities and relations are compressed in shorter code words – equations. These algorithms can be viewed as a whole class of encoding functions producing the shortest code words possible. As easily noticed, permutation among the symbols are not permitted without changing the encoded information.
Although the above discussion has been restricted to the processing of quantities, the same interpretation can be applied to different dimensions of perceptual information processing. Therefore different areas of applied mathematics are connected with different cognitive processing limits; e.g. geometry and size-constancy processing, differential calculus and object’s speed and trajectory processing, and so on. The interpretation also seems to give an explanation to the intuition “simple theories are the best theories”, for the simple theories’ costs are smaller, which decreases the probability of error. It’s by no mere chance that much of the mathematician’s work consists of, by exploring the isomorphism among different structures, finding simpler ways in which to solve a problem. However, it doesn’t always mean that complex theories can be compacted into simple (low cost) representation. In fact, according to the source coding theorem, the lower bound compression is the R(D), which is R(0)=H(X). Therefore, as long as one looks for less lossy representations, the code words’ cost inevitably is to increase.
Representations Stand for What?
The representational interpretation of the internal experience and the symbolic language’s role has dominated the occidental thought at least since Plato. The general idea of this line of thought seems to be grasped through the Varela et al. words:
“[…] that the world is pre-given, that its features can be specified prior to any cognitive activity. Then to explain the relation between this cognitive activity and a pre-given world, we hypothesize the existence of mental representations inside the cognitive system (whether these be images, symbols, or sub-symbolic patterns of activity distributed across a network does not matter for the moment).”39
In the representational interpretation, the particularities of a given representation – such as colors, extension, or commutativity – stand for real properties from the outside world and it is the relation of correspondence or adequacy, with its reference to the outside world that makes one representation better than another.[1] On the other hand, in the channel code interpretation of the representation’s role, a code’s intrinsic characteristics, for example, encoding light as colors or as wave lengths, has nothing to do with source information, all that matters is the source’s and code’s complexity. As we have seen, these particular coding aspects have rather a lot to do with channel and its cost, and not with the source itself. Speculatively, if the brain-cost capacity were greater (or infinity) than that suggested by cognitive experiments, the employment of symbolic language would be unnecessary.
What does it mean to say source and code complexity? The intuitive way to understand this complexity is in terms of the degrees of freedom of the system’s behavior or the degrees of freedom through which a system can affect another one. Mathematically, any system can be conceptualized as a set of variables and its degrees of freedom as a distribution of probability. If so, the Shannon Entropy, which is a function of the distribution of probability, emerges as a suitable measure of complexity in terms of the minimum bits necessary to describe unequivocally the system behavior.[2]; 8,40,41 More importantly, the main purpose of a code is to convey the source’s complexity as reliably as possible. However, very different codes can display the same complexity and their intrinsic characteristics will depend exclusively on the channel’s nature. But how can we evaluate the code’s performance? This is a very important question.
Footnote
a. [1]It is worth noting that in the representational interpretation, the belief that simple theories are better has, in principal, no clear explanation.
To evaluate the code’s performance, one has to measure the distance between the source information and the processing information, which is properly the source representation. This distance is measured according to a distortion measure whose definition depends on the system’s purpose. As we have said before, as the CNS is understood as a control system, the distortion measure has to be one that grasps this controlling dimension. In our model, the distortion measure is a Hamming-like distortion that we call Accident Function,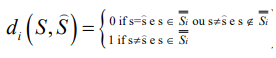 . The accident function interprets, as an error, the decoding which results in accident. Therefore, the symbol “=” does not represent “equals” or “equivalent” but represents successful action – the symbol “≠” is for unsuccessful action. Therefore, if two coding schemes result in the same source representation (action plans), they will be equivalent for communication purposes. The perspective seems to be in agreement with one of the older philosophical insights; that we cannot compare the reality with subjective or symbolic representation. However, all the time, we compare and test the motor plans and empirical experiments resulting from these coding schemes. When a given code directs us to a successful motor plan, we say that “it represents the reality”. Putting these two ideas together we get to the following statement: Our epistemology (coding schemes) can be diverse, but our ontology (successful interaction) is unique.
. The accident function interprets, as an error, the decoding which results in accident. Therefore, the symbol “=” does not represent “equals” or “equivalent” but represents successful action – the symbol “≠” is for unsuccessful action. Therefore, if two coding schemes result in the same source representation (action plans), they will be equivalent for communication purposes. The perspective seems to be in agreement with one of the older philosophical insights; that we cannot compare the reality with subjective or symbolic representation. However, all the time, we compare and test the motor plans and empirical experiments resulting from these coding schemes. When a given code directs us to a successful motor plan, we say that “it represents the reality”. Putting these two ideas together we get to the following statement: Our epistemology (coding schemes) can be diverse, but our ontology (successful interaction) is unique.
Conclusion
I have been discussing, broadly, different paths taken by an organism to better perform cognitive tasks. In this interpretation, these “paths” are understood as different coding schemes through which information is processed by the Central Nervous System. Two main aspects concerning the coding schemes’ performance were pointed out. These are the coding scheme’s cost and its ability to handle with redundancy. We distinguished among three coding schemes to which the organism resorts: the prompt processing, working memory, and the symbolic coding scheme. The prompt processing scheme seems to be the better code on average; however, a bad one for specific tasks. The working memory coding scheme seems to be better than the former one, but still too costly to perform specific tasks optimally. The symbolic scheme seems to be the cheapest and the more dynamic one for handling redundant information. The coding scheme metaphor serves to explain the old philosophical insight that simple theories are better theories and to mark a division between the epistemological domains as diverse versus the ontological domain as unique.
Footnote
a.[1]Shannon Entropy is not the only measure of complexity. The Kolmogorov-Chaitin complexity is also a measure of complexity and both measures are mathematically related.3,16,29
Consent Statement
Authors obtain written informed consent from the patient for submission of this manuscript for publication
Acknowledgements
We thank to CAPES, Coordenadoria de Aperfeiçoamento de Pessoal de Nível Superior (CAPES, Brazil) for financial support and the Department of Philosophy and Cognitive Science at University of California in San Diego (UCSD) for all support.


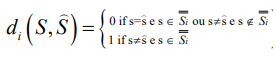 1.1.
1.1.



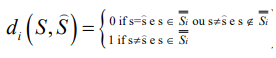 . The accident function interprets, as an error, the decoding which results in accident. Therefore, the symbol “=” does not represent “equals” or “equivalent” but represents successful action – the symbol “≠” is for unsuccessful action. Therefore, if two coding schemes result in the same source representation (action plans), they will be equivalent for communication purposes. The perspective seems to be in agreement with one of the older philosophical insights; that we cannot compare the reality with subjective or symbolic representation. However, all the time, we compare and test the motor plans and empirical experiments resulting from these coding schemes. When a given code directs us to a successful motor plan, we say that “it represents the reality”. Putting these two ideas together we get to the following statement: Our epistemology (coding schemes) can be diverse, but our ontology (successful interaction) is unique.
. The accident function interprets, as an error, the decoding which results in accident. Therefore, the symbol “=” does not represent “equals” or “equivalent” but represents successful action – the symbol “≠” is for unsuccessful action. Therefore, if two coding schemes result in the same source representation (action plans), they will be equivalent for communication purposes. The perspective seems to be in agreement with one of the older philosophical insights; that we cannot compare the reality with subjective or symbolic representation. However, all the time, we compare and test the motor plans and empirical experiments resulting from these coding schemes. When a given code directs us to a successful motor plan, we say that “it represents the reality”. Putting these two ideas together we get to the following statement: Our epistemology (coding schemes) can be diverse, but our ontology (successful interaction) is unique.