On the Destruction of Cancer Cells Using Laser-Induced Shock Waves: A Review on Experiments and Multiscale Computer Simulations

Martin Oliver Steinhauser, PhD

Department of Systems Solutions, Fraunhofer-Institute for High-Speed, Dynamics, Ernst-Mach-Institut, EMI, Eckerstrasse 4, 79104 Freiburg,Germany; Department of Chemistry, Faculty of Science, University of Basel Klingelbergstrasse 80, CH-4056, Basel, Switzerland, Tel. +49 761-2714-424; Fax: +49 761-2714-1424; E-mail: martin.steinhauser@emi.fraunhofer.de

INTRODUCTION

On a fundamental level, cancer is a complex disease which exhibits uncontrolled cell proliferation: cancer cells, either through epigenetic alterations or mutations, overexpress oncogenes and under-express tumor suppressor genes (TMGs). Hence, the cells go through the cell cycle more often, completely disregarding apoptotic signals, resulting in an increased proliferation and uncontrolled tissue growth.¹ Consequently, most cancer therapies attempt to manipulate these processes either by cytostatic (suppressing entry to or progression through the cell cycle) or cytotoxic (inducing apoptosis, programmed cell death) mechanisms. For example, chemotherapy agents such as doxorubicin are considered to be cytotoxic.² Therapies that target hormone-addicted cells (e.g., tamoxifen in estrogen-driven breast cancer) are considered to be cytostatic.³

The Physics of Cancer Cells

Studies of cells’ passive viscoelasticity-based biomechanics have already led to deep insight into a cell since its mechanical properties are directly related to its function by the cytoskeleton composition and architecture.⁴ Intracellular pathologic changes influence cytoskeleton structure and function, which makes a cell’s mechanical signature a highly sensitive marker of its health.⁵ In malignant cells the cytoskeleton devolves from an ordered and rigid structure to an irregular and compliant state, including a reduction of the cytoskeleton polymers and accessory proteins and a restructuring of the network. The cell changes from a mature state to a replicating, motile and cancerous form.⁶ From a more general viewpoint, cytoskeleton strength and organization increase as a cell becomes more differentiated. Thus, stem cells and malignant cells, as undifferentiated cells, are expected to be softer than mature and fully differentiated cells. Consequentially, measuring a cell’s rigidity provides information about its state and composition and may be viewed as a cell marker.⁵ In recent years, genetic, immunocytochemical and biochemical studies have identified many different players involved in the regulation of the cytoskeleton. Physical studies concentrating on the mechanical properties of cells or in vitro cytoskeleton model systems have been helpful in elucidating the complex synergies and redundancies of generic physical and specific biological mechanisms in establishing the overall mechanical performance of biological tissue. Unexpectedly, such studies have revealed a remarkable universality in the viscoelastic response functions of reconstituted networks and of whole cells of different types over a wide range of timescales, which is reminiscent of glassy materials.^7,8 At the same time, the overall cell stiffness has been demonstrated to be very sensitive to cytoskeleton dysfunction, a connection that lends itself to an extremely efficient and reliable automated detection (and may possibly also be the cause) of some diseases.⁵ To gain a detailed understanding of  how these highly universal and specific mechanical properties of cells originate from the molecular structure of the cytoskeleton, it is essential to probe cell mechanics on multiple scales.

Treatments of Cancer

Traditionally, the only cure for solid tumors has been surgery, i.e. the resection of solid tumor tissue.⁹ However, open surgery is always associated with a high risk for the patient, suppression of a patient’s immune system and a significant mortality rate. Minimally invasive techniques as an alternative to open surgery, which became available during the 1990’s for localized tumor treatment, such as radiofrequency ablation,¹⁰ cryoablation,¹¹ direct laser ablation,¹² or high-intensity focused ultrasound (HIFU), are methods which use a range of energies for direct in situ tumor destruction through energy absorption and killing by heating or evaporation. Besides direct conversion of mechanical energy into heat, biological material may be damaged by the effects of mechanical stress caused by shock waves.¹³  An efficient way to generate shock waves in biological systems became available to biomedical research by the use of high-power lasers shortly after the invention of the Q-switched pulsed laser in the 1960s.¹⁴

The Impact of Shock Waves on Cells

The theoretical foundations of shock wave physics originated from 17^th century studies of classical acoustics and 18^th century aeroballistics. With the advent of high-speed photography in late 19^th century and further progress in experimental visualization techniques in 20^th century, the study of shock waves in different states of matter has gradually emerged from a very small and unnoticed branch of physics to a major complex and interdisciplinary science.^15,16

Physical Definition of Shock Waves

Shock waves are in essence discontinuous, rapid mechanical phenomena that have been observed and studied in the laboratory and in nature, in microscopic as well as in macroscopic dimensions and in all states of matter: gaseous,^17,18 liquid,^19,20,21 solid,^22,23,24 plasma,^25,26 and even in Bose-Einstein condensates.^27,28,29 Terrestrial examples³⁰ of naturally occurring discontinuities are high-energy events such as meteorite impacts, thunder, volcanic explosions, sea-and earthquakes or tsunamis, while in outer space³¹ they encompass plasma shock waves induced by solar wind, supernovae explosions, implosions of white dwarfs, comet and asteroid impacts, and stellar or galactic jets. This variety of phenomena and in particular the possible applications of shock waves in different areas such as physics, chemistry, biology, medicine and even engineering generally renders the scientific study of shock waves a rather fascinating and interdisciplinary subject.

We focus here on the physical proper definition of shock waves which–in medical literature–is not always used correctly and many studies fail to show that they were really dealing with shock waves and not merely with high-energy sound waves. In the natural sciences, a shock wave describes a mechanical wave characterized by a surface or sheet of discontinuity in which, within a narrow region, thermodynamic quantities such as pressure p, density ρ, particle velocity v or temperature T change abruptly.¹⁷ While a theory of shock waves with an infinitesimal jump condition can be developed mathematically in the framework of approximate continuum models of condensed matter, i.e. based on the hydrodynamic equations of ideal fluids or gases, in physical context, shock wave theory is somewhat limited, because the width of a shock wave is always of finite size and because of the actually discrete atomic nature of condensed matter. It turns out that shock waves are essentially small regions of a system, where non-adiabatic, i.e. irreversible energy dissipation occurs. The notion of a shock wave as an infinitely thin sheet of discontinuity is a mathematical idealization. The width of the shock wave i.e. the size of the dissipative region establishes itself according to the conservation laws of continuum theory. In very strong, high-amplitude shock waves, their width becomes so small that they are practically indistinguishable from the mathematical idealization of an infinitesimally small perturbation with jump conditions for thermodynamic variables.

In solids, physical shock waves are mechanical waves of finite amplitudes and arise when condensed matter is subjected to a rapid compression. Shock waves can be defined by several major distinctive properties as follows:

• A pressure-dependent, supersonic velocity of propagation.
• The formation of a steep wave front with a sudden change of thermodynamic quantities.
• Non-linear superposition properties (for reflection and interaction).
• A strong decrease of propagation velocity with increasing distance from the center of the origin for the case of non-planar shock waves.

Sometimes another criterion for a shock wave is listed in shock wave literature which is the extremely short rise time of the pressure within tens of nanoseconds. However, this is not a defining criterion of shock waves, because no generally agreed upon definition exists of what “extremely short” really is supposed to mean – it is a term of rather subjective nature. A nanosecond rise time certainly applies for lithotripter shock waves which are used in medicine as a non-invasive technique to comminute calculi³² and for other therapeutic purposes³³; however, in the geologic realm for example, meteorite impacts, explosive volcanic eruptions and earthquakes can provoke drastic and irreversible changes within seconds.

One characteristics that distinguishes a shock wave from an ordinary sound wave is that the initial disturbance in the medium that causes a shock wave is always traveling at a velocity greater than the phase velocity of sound in the medium (the electromagnetic analog of this is called Cherenkov radiation).³⁴ Because a shock wave moves faster than the speed of sound, the medium ahead of the shock front cannot respond until the shock strikes, and so the shock wave falling upon the particles of matter initially at rest, is a supersonic phenomenon.

Shock Waves Produced by Lithotripters

Since its invention in the early 1980s, Extracorporeal Shockwave Lithotripsy (ESWL) has evolved as a clinical standard, which is widely used as the only non-invasive surgical technique to eliminate e.g, kidney stones and other urinary calculi.³³ Rassweiler et al³⁵ describe the multiple mechanisms associated with stone disintegration by ESWL as well as current advances in instrumentation and clinical praxis. A shock wave is a mechanical wave that induces a transient pressure rise and propagates at a speed above the speed of sound of the corresponding medium. It is created by means of a piezoelectric, electro-hydraulic or electromagnetic transducer, called lithotripter, which generates focused high-amplitude pressure waves in a contact medium outside the body.^35,36 The patient is positioned such that the stone is brought into the focus of the pressure wave. When the acoustic energy deposited in the focal region is high enough, cavitation bubbles filled with vapor or gas form and collapse violently. This collapse results in formation of a shock wave that in turn disintegrates the stone. Apart from stone destruction, ESWL can cause tissue injury as unwanted adverse effects during treatment.³⁷ The physical mechanisms related to the cavitation phenomenon that cause both stone destruction and tissue damage are very complex, not well understood and hardly experimentally controllable.^35,37,38,39 The fact that ESWL can cause tissue damage, inspired experiments that applied lithotripter induced shockwaves to tumors in vivo. While several first studies in animal models did not show any impact of shock waves on tumor growth,³⁶ some results seemed encouraging, for example a delayed tumor growth in mice⁴⁰ and even complete remission of dorsal skin tumors in hamsters.⁴¹ However, up-to-date shock wave treatment has not been used in clinical traits, most likely because the cavitations phenomenon is very hard to control and the unspecific effects on ESWL on cells cause the need for live imaging techniques during treatment. Parallel to the in vivo experiments on tumors, a large number of in vitro studies on different cell lines in culture were performed as reviewed by Coleman and Saunders,³⁶ and Delius.³⁹

The application of several hundred shock waves created by commercial lithotripter systems causes cell death. Most striking for a possible shock wave based tumor therapy was a study on different normal and malignant cell lines, which showed no selective effect.³⁸ When the energy deposited by the lithotripter is reduced below the lethal value, it is possible to permeabilize the cells without killing them.^{42,43,44,45,46} In this way, molecules present in the surrounding medium can diffuse into the cells. This effect has possible applications for drug delivery and gene transfer.⁴⁷ In more recent studies, adherently grown cells on transparent substrates were exposed to shock waves and analyzed with (fluorescence) microscopy. In direct vicinity of the cavitation bubble, the cells are completely destroyed and detached from the surface. Cells close to the bubble were permanently permeabilized and killed, whereas cells further away from the bubble survived.^48,49 This behavior could be connected with deformations of the cytoskeleton.⁵⁰ Generally speaking, ESWL treatment of cells seems to be only poorly controllable because of the cavitation process and no selective effects on cells are observed. These disadvantages might be overcome by the technique of laser-induced shockwave generation discussed in the next section, which is based on purely mechanical destruction of cells, where no cavitation effects occur.

Laser-Induced Shock Waves

When irradiating an absorbing material with a pulsed laser, the optical energy deposited on the absorber is transformed into mechanical energy. A shock wave forms at the surface and then travels the absorber.⁵¹ The shock wave properties such as rise time, velocity of propagation or peak pressure depend on the absorbing material and the laser parameters. For one specific laser/absorber system, the peak stress of the shock wave can be tuned by varying the laser fluence that is equal to the total energy deposited per area of illumination.^52,53,54 In this experimental configuration, well-defined, reproducible shockwaves can be generated without the side effect of heating or cavitation.⁵⁵ Thus, the pure mechanical effect of the shockwave on the cells can be investigated. As reviewed by Yao et al,⁵⁶ also Laser-Induced Shockwaves (LISW) are able to render the cell membrane permeable, giving rise to drug delivery and gene transfection. The application to whole tissue structures is also possible. For example, transdermal insulin delivery by LISW results in a reduction of the blood glucose level without causing any pain to the patient.⁵⁷ Here, we focus on the direct lethal effect of LISW on cells. In the following, we review the literature concerning the impact of LISW on cells and present current progress and novel developed techniques that will help to further classify the properties of LISW.

In Table 1, we provide an overview of major studies that investigated the biological effects of the interaction of shock waves (or strong pressure waves) with biological cells.

Figure 1 shows the basic features of the experimental setups used in several studies reported in the literature.^{60,61,62,65,66,69} The laser beam is directed onto the bottom of a cell culture vessel, that consists of an absorbing material. Upon illumination with the laser, a shock wave is formed that travels into the vessel, and interacts with the cells. For one specific cell line, it turned out that the survival rates of cells exposed to LISW depend on stress gradient σ=p_max/τ_R, where p_max is the peak pressure and  is the rise time of the shock wave.⁶⁰ However, the survival rates among different cell lines differ remarkably at constant physical parameters p_max and τ_R. For example, only 50% of transformed (immortalized) retinal pigment epithelium cells survive exposure to shock waves with p_max=74 MPa and τ_R=10 ns. However, 100% of normal retinal pigment epithelium cells survive this procedure.⁶⁰ A shock wave with τ_R=10 ns and p_max=30 MPa kills 50% of mouse breast sarcoma cells, whereas human promelocytic leukemia cells survive this exposure.⁶⁹

Figure 1: (a) Basic elements of the experimental setups used to study the effects of laser induced shock waves on cells.^{36,49,50,51,52,53} (b) A pulsed laser beam irradiates an absorbing material at the bottom of the vessel (usually a polymer) that contains the cells and their growth medium. At the surface of the absorber, a shock wave is formed that moves forward into the vessel. When the absorbing material is covered with a transparent material facing the laser, the peak pressure of the shock wave is further enhanced.⁵³ In recent breakthrough experiments, Schmidt et al72 managed to optimize this setup by using standard multi well culture vessels and black varnish as absorber material. Pressure levels in the cells beyond 80 MPa were achieved, which is well above the pressure levels in all previous studies reported in literature.

All of the above mentioned studies in Table 2 had major deficiencies in the techniques used to characterize the physical conditions in the vessel. Usually, the pressure profiles are measured with piezoelectric elements (Polyvinylidene fluoride, PVDF) either in form of needle hydrophones or piezoelectric films that are brought in contact to the surface of the culture vessel. In both cases, a transfer medium (either water or grease) serves as the acoustic contact to the piezoelectric element. However, shock waves are known to decay very rapidly (within micrometers) in liquids and tissue.⁷⁰ Thus, the need for a fluid as contact medium may lead to wrong pressure measurements and it would be desirable to determine shock wave properties on a microscopic scale, rather than with a PVDF sensor of millimeter dimensions. An alternative to determining the pressure profiles with piezoelectric element is to use optical methods that measure the velocity profile of the vessel bottom while the shockwave passes. From this velocity profile the pressure profile in direct vicinity of the bottom plate can be calculated. This informationis particularly interesting when studying adherently grown cell cultures. Strand et al⁷¹ developed a cost efficient and compact high-speed velocimetry system that uses a heterodyne detection method.

An optical fiber is used to transport Laser light to a probe that contains a lens. The light is then focused onto the moving surface that reflects or scatters light back into the probe from where it is brought to a detector. The frequency of the light is now Doppler-shifted because of the surface movement. At the detector, it is mixed with non-Doppler shifted light to generate a beat signal that contains the velocity information of the moving surface. In a recent breakthrough application, velocity profiles have been measured in this way and could also serve as input for simulations that computed the pressure fields within the whole vessel with high time resolution.⁷² In this way, the conditions that the cells are exposed to during the shock wave experiment can be characterized on the relevant length and time scales which are micrometers and nanoseconds. For beam diameters of a few millimeters, in the author’s laser lab, with an optimized experimental setup, peak pressures up to approximately 120 MPa were obtained which is considerable beyond the pressure levels of all previous studies discussed in literature, see Figure 2.

Figure 2: Optimized setup used in recent breakthrough experiments by Schmidt et al.⁷² (a) Ordinary multiwell cell culture plates were used (positioned here on an optical table) and U87 glioblastoma cells were grown adherently on the bottom of the individual wells. The achieved pressure levels were measured directly in the wells by means of PVDF hydrophones with nanosecond time resolution. (b) By using black varnish as absorber material, it was possible to reach pressure levels in the cells beyond 100 MPa which is well above the pressure levels achieved in all previous studies reported in literature. For U87 glioblastoma, it was found that a biological destructive effect occurs
above 80 MPa, which is a pressure level well above the ones achieved in all previous experimental studies reported in literature, cf. Table 1. One great advantage of the setup shown here, is its reproducibility in both, the pressure level measurement by using very well-defined single laser pulses per well and the level of destruction in the cells which was verified by cell counting and a long term MTA-analysis over several days, i.e. over several cell cycles with negative results (i.e. no destruction) in the untreated controls.

COMPUTATIONAL MULTISCALE MODELING OF CELLS AND TISSUES

Exploring the potential of shock waves for destroying or damaging cancer cells possibly opens a new or complementary road for tumor treatment, avoiding the disadvantages of currently established methods for tumor treatment based on US, and using only the mechanical destructive effects of a shock wave interacting with cells. By way of using the mechanical effects of shock waves rather than relying on heating of tissue, it seems possible to destroy or damage the cytoskeleton or the membrane, as shock waves carry much more energy in a much shorter time interval than US waves do. This might open new perspectives for cancer therapies in addition to existing treatments. The complexity occurring in the interaction of shock waves with soft, biological matter requires a combined approach using experimental and numerical methods which is exemplified in Figure 3. To model the mechanical properties of eukaryotic cells, a focus is set on the two salient features of cells that determine their mechanical behavior: the cytoskeleton (composed of a network of macromolecules) and the plasma membrane (composed of double lipid layers).

Figure 3: An integrated approach combining the full complexity of the real experimental system with computational coarse-grained (CG) models of extremely reduced complexity. In CG models, typically, only two major components of cells determining their mechanical properties relevant for their interaction with shock waves are considered: The plasma membrane and the cytoskeleton. Figure taken from Steinhauser.⁷³

Considered from a physical perspective, living organisms such as eukaryotic cells or neoplasia are far more complex systems than typical engineering materials such as metals, ceramics, polymers or semiconductors, see Figure 4. They are dynamic and provide integrated functions that include metabolism, reproduction, growth, sensing, communication, control, and apoptosis (programmed cell death).

Figure 4: Multistage aspects of different classes of engineering and organic materials, i.e. of
condensed matter. Living organisms involve many different features on different length and
time scales. Both, engineering materials and living matter are made from the same constituents, i.e. atoms being held together by chemical bonds. Figure taken from Steinhauser.⁷⁷

Different studies have established the connections between structure, mechanical responses and biological functions of different organs and tissues including, for example, the heart, lung, bone, cartilage, blood vessel, and skeletal and cardiac muscles.⁷⁴ These studies have led to better diagnosis and treatment of orthopaedic, cardiovascular and respiratory diseases by providing a greater understanding of how the biological functions of the body are related to bio-solid and bio-fluid mechanics. To decipher the fundamental mechanisms of biological materials, however, more systematic studies of deformation, structural dynamics and mechanochemical transduction in living cells and biomolecules are needed. The mechanics of biological molecules, including proteins and nucleic acids, is crucial to understanding the connection between structure and function in cellular and tissue mechanics. Still in its infancy, this emerging field of bio-mechanics strives to understand the deformation and mechanics of macroscopic tissue structures based on the deformation and mechanics of bimolecular. A recent summary of current multi scale simulation approaches for bridging the scales from sub-cellular components to tissue is provided in a recent review by Steinhauser.⁷³

MECHANICAL PROPERTIES OF COMPLEX MATERIAL SYSTEMS

Upscaling of atomistic and microscopic simulation approaches of the kind as displayed in Figure 5, is one way of trying to understand the basics of shock wave effects on soft matter systems such as cells and living tissue.⁷⁵ There are a number of complex microscopic systems, which are relevant to the study of animal or human cells, and which form the basis of any physical, and mathematical-numerical modeling, since the systems we are interested in build a complex system made of polymer melts and solutions, suspensions, gels and micelle systems. The microstructure of these systems is very important for the elaboration of constitutive equations on a coarse-grained, phenomenological level.

In Table 2, we review and summarize some of the key rheological properties of a few of these systems. For example, polymers are viscoelastic and may become viscoplastic in some cases when they form a gel (polymer network). They are present in a cell in the form of proteins and play a fundamental role for many cell functions and cell-cell interactions. The basic microstructure of a polymer network consists of chains intermingled with each other (entanglements) with a few weak reticulation points, as well as loops or dangling ends.⁷⁶ Gel materials are interesting systems, because the cell cytoplasm may be regarded as a gel. Elastomers are slightly different and may be considered as viscoelastic solids, in particular, because they cannot flow at very low shear rates. This is mainly due to strong links (covalent sometimes) associating polymer chains thus creating a network which behaves elastically over a wide range of shear rates.

On the nanoscale, their microstructure looks something like a regular net. As the frequency is increased, they undergo a glassy transition where moduli G’ and G” behave as ωⁿ, where  n is an exponent whose value is close to 0.6. Polymer solutions are solutions containing polymers in a solvent and do not exhibit entanglements in this regime. They may be considered to have two components, one being the solvent (which is viscous with constant viscosity η) and the other one being the polymer with viscoelastic properties. The field of suspensions is quite large, because it can describe particulate suspensions, but can also lead to fluid-fluid suspensions called emulsions, and all kinds of systems including deformable objects in a fluid. For example, blood is a mixture of white and red blood cells, platelets and other constituents included in the plasma.

Most of the biological cells are 1-100 microns in size, and they comprise many constituents, Figure 5. The cell is covered by a phospholipid bilayer membrane reinforced with protein molecules, and the interior of the cell includes a liquid phase (cytosol), a nucleus, the cytoskeleton consisting of networks of microtubules, act in and intermediate filaments, organelles of different sizes and shapes, and other proteins, Figure 5. The resistance of single cells to elastic deformation, as quantified by an effective elastic modulus, ranges from 102 to 105 Pa, see Figure 6, which is orders of magnitude smaller than that of metals, ceramics and polymers. The deformability of cells is determined largely by the cytoskeleton, whose rigidity is influenced by the mechanical and chemical environments including cell-cell and cell-Extracellular Matrix (ECM) interactions.

Figure 5: Microscopic modeling and simulation approaches for the cytoskeleton and the amphiphilic plasma membrane of eukaryotic cells.(a) Image of a mouse NIH3T3 fibroblast cell, fixed and stained for DNA (blue) and the major cytoskeleton filaments act in (red) andalpha-tubulin (green). Figure reproduced with permission from Suresh et al.⁴ (b) Modeling approach for the cytoskeleton as a meshed network of polymers. Simulation snapshot generated in the Steinhauser-lab with the molecular dynamics software-suite MD-CUBE,⁷⁸ showing a stretched three-dimensional polymer network.⁷⁹ Color code indicates forces in the bonds of the polymers with red: very large force just before bond failure, and green: force-free bonds. (c) A simulation of the self-assembly of a threeparticle amphiphilic lipid model (hydrophilic part of the lipid: red, hydrophobic part: yellow) where the lipids self-assemble to form bilayers. Subsequently, these equilibrated bilayers are exposed to strong shock waves.⁸¹Simulation snapshot adopted from Schindler et al.⁸⁰

Figure 6: Approximate range of values for the elastic modulus of biological cells and comparisons with those of engineering metals, ceramics and polymers.

If the elastic, visco-plastic properties of the basic constituents of cells and tissue are known, there is a variety of techniques to produce constitutive equations for a macroscopic description, such as ensemble averaging,^88,89 mathematical homogenization,⁹⁰ effective medium theory,⁹¹ or temerity models which are based on the idea to model deformable structures by using sticks and strings under tension.^{92,93,94,95,96,97}

It was shown that this approach is particularly well adapted for the description of eukaryotic biological cells.⁹⁸ However, the previously listed techniques are usually not able to account for specific interactions between cells, their individual, specific behavior or the active response of cells to external stimuli.

Another, more direct way of modeling shock wave effects in tissue and cells is to use macroscopic models based on continuum theory rather than upscaling basic properties. Continuum models, e.g. based on finite elements meshes neglect almost all details of the discrete nature of the constituents of cells and tissue but allow for a macroscopic simulation of deformation upon exposure to shock waves. The quality of these type of simulations however, is very strongly depending on the employed phenomenological material model and additional complexity is to be considered here, because of the local heterogeneity of tissue and a general lack of experimental measurements in vivo. Generally speaking, it is at least questionable, whether experimental in vitro studies of tissue behavior have real physiological relevance.

MECHANICAL PROPERTIES OF SOFT BIOLOGICAL TISSUES

For many years, researchers have devoted their attention to the study of animal tissues, and important issues have been raised. Finding constitutive relations for such media is not simple, because tissues can behave as elastic, plastic, viscoelastic or viscoplastic materials. One of the most important conclusion is that relating the microstructure with its macroscopic nature is a fundamental problem which forms the basis of any continuum mechanics problem.⁸³ The relevant sciences studying such aspects are rheology^83,99,100 and biomechanics.^{101,102,103,104}

These two fields are actually very close to each other when it comes to dealing with biomaterials, and defining their minor differences here is not my intention. One may say that generally one is interested in finding relationships between the applied forces and the relevant deformations or flows involved in problems dealing with living materials. Classical models (1D), which can be used and can depict the cytoplasm of a cell, are usually viscoelastic or viscoplastic ones. 3D-viscoelastic models can exhibit differential forms, or integral formulations (sometimes equivalent). Other models like viscoplastic ones can also be interesting because they allow us to deal with systems with cross-links, somehow close to gels; in particular, polymers and networks play a role inside the cytoplasm, Figure 5a and 5b. So, at a certain level, we may assume that the size of the system studied  is large enough , where is the size of an element at the microscopic level, so that the system exhibits a macroscopic, averaged behavior and can be described using a constitutive relation as it is done in typical, empirical engineering approaches for material modeling.

Generally speaking, material models have to include the following material behavior (listed in increasing order of complexity):

1. Linear elasticity.
2. Hyperelasticity.
3. Hyperviscoelasticity.

Many computational approaches only include hyperelasticity. The general description from which such models start, is the Ogden hyperelastic material model¹⁰⁵ which assumes the existence of a strain energy function  in the form:

where are the principal stretches, n and α_p are material constants, and μ_p denotes the shear modulus of the material in the undeformed state. We note that the often used Mooney-Rivlin material model,^106,107 which assumes that  can be written as the sum of two invariants, is contained in the above formula as a special case.

Therapeutic technologies such as focused US and shock wave treatment, have an extremely localized area of therapeutic effect and therefore have to be applied directly over specific location of anatomic/functional abnormality, precisely in relation to the current (i.e. intra-operative) patient’s anatomy. As surgical intervention tends to distort the pre-operative anatomy and often leads to misalignment between the actual position of pathology and its position determined from pre-operative images, an image-guided surgery requires intra-operative images and/or update of the pre-operative images to the current position of the brain internal structures. To achieve an accurate image update, deformations of the abdominal organs (e.g. the brain, the liver or the kidneys) must be taken into account. Since the late 1990s, significant research effort has been directed towards the prediction of such deformations using biomechanical models.^{108,109,110,111,112,113,114,115} Typically, in such models, the Finite Element (FE) method^{116,117,118,119} is employed to discretize and solve the related differential equations of continuum mechanics, see Figure 7. During image-guided surgery, only low-quality, sparse information about the current tissue position is available.¹²⁰ This information can be used to warp high-quality pre-operative images, such that they correspond to the momentary situation, by computing the deformation field within the brain using a biomechanical constitutive model.

Figure 7: FE applications for modeling the deformation of tissue as a reaction to being exposed to shock waves. (a) FE model of specific meshes of a left hemisphere of a human brain including ventricles and tumor (red). The entire mesh comprises of 16,925 nodes, 15,031 hexahedral (8-noded bricks) and 19 pentahedral elements. The elements’ characteristic length varied between 0.6 and 6 mm. (b) From left to right: Typical kidney injuries after an ESWL treatment observed on an adult pig kidney,¹²¹ and the computed field of irreversible volumetric expansion in an exterior view. Meridional section of a anatomically correct finite element mesh of the kidney. The photograph illustrates how difficult it is to generally quantify the amount of tissue injury.

In a comparative study by Wittek et al¹¹⁴ it was shown that the actual choice of a specific material model hardly influences the calculated displacements of tumors. Between different models, the differences in displacement amounted to less than 0.2 mm. It seems that the organ displacement is dominated by its weak compressibility rather than the resulting stresses. Many different experimental setups and different theoretical descriptions are used to extract mechanical parameters from tissue measurements. We end this review by listing the results of various such studies in Table 3. One way of comparing these different results is to calculate Young’s modulus based on local linear elasticity.

CONCLUSIONS AND FUTURE PERSPECTIVES

As a clinical tool, within its limits of applications, HIFU is established as a therapeutic tool. As this technique becomes more widely available, it should be possible to coordinate the type of clinical trials that will be necessary to develop the evidence base for the efficacy of HIFU in its various applications, whether alone or in combination. Real-time imaging and treatment monitoring are the subjects of ongoing theoretical research, and the development of techniques such as three-dimensional ultrasound and elastography which measures the change in stiffness of a tissue as it is ablated, are likely to enable improvement in clinical outcome and to bring about a reduction in treatment duration. In addition, focused ultrasound has been proposed as a vehicle for delivering targeted gene therapy through inducing cavitation of DNA-laden micro bubble contrast agents in the periphery of the zone of ablation, where temperature rises would be sublethal, but these remain secondary considerations to the direct ablative treatment intent at present.

The experimental observation that shock waves are able to destroy cells in vitro and to delay tumor growth in vivo motivates further studies of the responsible mechanisms. The author believes that characterization of shock wave impact on the cellular level is necessary to understand these processes more systematically. Laser-induced methods for shock wave generation have proven to be reproducible on the macroscopic level and to avoid lithotripter related side-effects such as heating and cavitation. Newly developed optical methods together with multiscale modeling approaches can give insights on the precise conditions that the cells are exposed to during shock wave impact. The knowledge of these conditions is a prerequisite to find and maybe control selective effects oncells. The diverse behavior shown by different cellular strains poses the need to find quantities that relate cellular properties with shock wave induced killing. Thus, in parallel to shockwave experiments on different cell lines, specific quantities have to be found that relate cellular properties with shockwave impact. Of course, mechanical properties related to the cytoskeleton serve as a first promising candidate and may by determined with combined cell-mechanical and fluorescent microscopic observations. In addition to the experiments on cells, another possible application of shock waves emerges from current biological findings that relate tumorous growth to mechanical properties of tissue. It has long been known that tumors are more stiff than healthy tissue. This fact is even used to detect mammary cancer, for example by palpation or elastography of rigid tissue structures. The mechanical properties of tissues are mostly influenced by the ECM, which mainly consists of collagen. These molecules are produced inside the cells and delivered to the ECM where they form polymeric structures that serve as scaffolds for the cells. When healthy tissue turns into a tumor, the polymeric structure of collagen fibrils is significantly altered, causing a stiffening of the ECM.⁸¹ Cells possess mechanoreceptors that detect physical forces and transform them into biochemical signals.⁸² Thus, cells are able to both sense and alter the mechanical properties of the ECM.⁸³ Interestingly, the biochemical signaling pathway of the mechano-sensing apparatus cross-talks with major pathways that control cell proliferation and it was shown that tissue stiffness promotes cancerous cell growth.⁸⁴ In this way, ECM stiffening and tumor growth form a positive feedback loop that enhances the risk of tumor formation.⁸² On the other hand, these current findings may open new possibilities of cancer therapy basing on mechanical methods, i.e. based on the physics of cancer rather than or in addition to pharmaceutical treatments. One of these interesting possibilities of shock waves therapy based on mechanical effects alone, is its potential to be used for gene transfection and molecular drug delivery, which involves interesting physical chemistry research concerning the structure of molecules to be used as drug carriers.⁸⁵

Within the biological sciences, cancer is highlighting the need for interdisciplinary research. There is a growing realization that cancer is a problem requiring input from a wider community of scientists, i.e. physicists, mathematicians and computer engineers. This is reflected in increasing interdisciplinary collaborations around the world, involving biologists, clinicians, physicists, mathematicians and computer scientists, which aim to give new insights into cancer and improvements in its treatment.

In a fashion quite analogous to studies of mechanics of engineering materials, the emerging field of cell and molecular mechanics of biological materials seeks to establish essential linkages between microscopic structure and macroscopic mechanical properties. New multiscale computational approaches have emerged in recent years, coupling e.g. atomistic scale simulations with the macroscopic domain as reviewed in Steinhauser⁷⁶ and also new numerical approaches combining coarse-grained macromolecular models of bio-molecules with shock wave physics emerged.⁸⁴ Although methods have been developed to measure cell responses during deformation, celladhesion, locomotion and mitosis, reliable experimental tools are currently unavailable for quantifying the distribution of mechanical forces between various subcellular structures as well as on individual proteins and nucleic acids inside a cell.

In summary, progress in experimental and computational biology and biomechanics during the past decade has provided unprecedented opportunities to probe the mechanical responses of cells, proteins and DNA molecules. How the forces and deformations associated with these basic structural units of life can be described by physical models, engineered by chemistry and implemented in computer programs, is a topic of substantial scientific excitement and interdisciplinary opportunity.

ACKNOWLEDGEMENTS

The author acknowledges financial support of the Fraunhofer-Gesellschaft, ex., Germany, under grant No. 600016 (Shock Wave Induced Destruction of Tumor Cells), and grant No. 400017 (Extracorporeal, Focused Ultrasound Therapy: Effectiveness, Simulation, and Planning of New Therapies). Interesting discussions with Constantin Coussios from Oxford University in the UK during my visit there, are gratefully acknowledged.

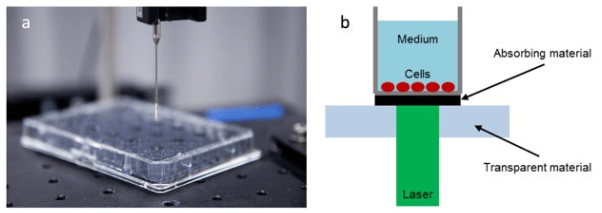
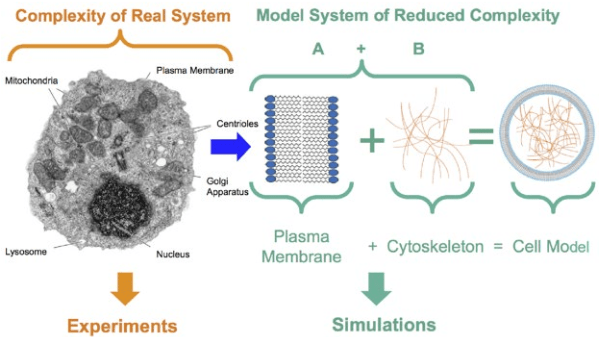
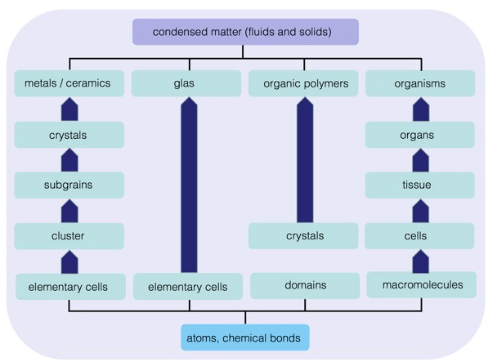
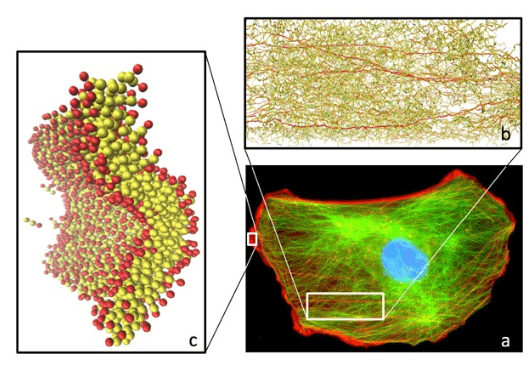
1. Mendelsohn J, Howley PM, Israel MA, Gray JW, Thompson CB. The Molecular Basis of Cancer. Philadelphia, PA, USA: Elsevier Science; 2014.

2. Blagosklonny MV, Robey R, Bates S, Fojo T. Pretreatment with DNA-damaging agents permits selective killing of checkpoint-deficient cells by microtubule-active drugs. J Clin Invest. 2000; 105(4): 533-539. doi: 10.1172/JCI8625

3. Pearson OH, Manni A, Arafah BM. Antiestrogen treatment of breast cancer: An overview. Cancer Res. 1982; 42(8 Suppl): 3424s-3429s. Web site. http://cancerres.aacrjournals.org/content/42/8_Supplement/3424s.short. Accessed July 24, 2016

4. Suresh S. Biomechanics and biophysics of cancer cells. Acta Biomater. 2007; 3(4): 413-438. doi: 10.1016/j.actbio.2007.04.
002

5. Guck J, Schinkinger S, Lincoln B, et al. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys J. 2005; 88(5): 3689-3698. doi: 10.1529/biophysj.104.045476

6. Fuh G, Cunningham BC, Fukunaga R, Nagata S, Goeddel DV, Wells JA. Rational design of potent antagonists to the human growth hormone receptor. Science. 1992; 256(5064): 1677-1680. doi: 10.1126/science.256.5064.1677

7. Gardel ML, Valentine MT, Crocker JC, Bausch AR, Weitz DA. Microrheology of entangled F-actin solutions. Phys Rev Lett. 2003; 91(15): 158302-158302. doi: 10.1103/PhysRevLett.91.158302

8. Gardel ML, Schneider IC, Aratyn-Schaus Y, Waterman CM. Mechanical integration of actin and adhesion dynamics in cell migration. Annu Rev Cell Devel Biol. 2009; 26: 315-333. doi: 10.1146/annurev.cellbio.011209.122036

9. Dunn BB. Cancer: Solving an age-old problem. Nature. 2012; 483(7387): S2-S6. doi: 10.1038/483S2a

10. Lackey L, Peterson C, Barr RG. Contrast-enhanced ultrasound-guided radiofrequency ablation of renal tumors. Ultrasound Q. 2012; 28(4): 269-274. doi: 10.1097/RUQ.0b013e318274de66

11. Goyal J, Verma P, Sidana A, Georgiades CS, Rodriguez R. Single center comparative oncologic outcomes of surgical and percutaneous cryoablation for treatment of renal tumors. J Endourol. 2012; 26(11): 1413-1419. doi: 10.1089/end.2012.0244

12. Vogl TJ, Straub R, Eichler K, Söllner O, Mack MG. Colorectal carcinoma metastases in liver: Laser-induced interstitial thermotherapy-local tumor control rate and survival data. Radiology. 2004; 230(2): 450-458. doi: 10.1148/radiol.2302020646

13. Suhr F, Delhasse Y, Bungartz G, Schmidt A, Pfannkuche K, Bloch W. Cell biological effects of mechanical stimulations generated by focused extracorporeal shock wave applications on cultured human bone marrow stromal cells. Stem Cell Res. 2013; 11(2): 951-964. doi: 10.1016/j.scr.2013.05.010

14. Carome EF, Clark NA, Moeller CE. Generation of acoustic signals in liquids by ruby laser-induced thermal stress transients. Appl Phys Lett. 1964; 4(6): 95-97. doi: 10.1063/1.1753985

15. Krehl POK. History of Shock Waves, Explosions and Impact: A Chronological and Biographical Reference. Berlin, Germany: Springer; 2009.

16. Steinhauser MO, Hiermaier S. A review of computational methods in materials science: Examples from shock-wave and polymer physics. Int Mol Sci. 2009; 10(12): 5135-5216. doi: 10.3390/ijms10125135

17. Rodriguez V, Saurel R, Jourdan G, Houas L. Solid-particle jet formation under shock-wave acceleration. Phys Rev E Stat Nonlin Soft Matter Phys. 2013; 88(6): 063011. doi: 10.1103/PhysRevE.88.063011

18. Zheng J, Chen QF, Gu YJ, Chen ZY. Hugoniot measurements of double-shocked precompressed dense xenon plasmas. Phys Rev E Stat Nonlin Soft Matter Phys. 2012; 86(6): 066406. doi: 10.1103/PhysRevE.86.066406

19. Falk K, Regan SP, Vorberger J, et al. Comparison between x-ray scattering and velocity-interferometry measurements from shocked liquid deuterium. Phys Rev E Stat Nonlin Soft Matter Phys. 2013; 87(4): 043112. doi: 10.1103/PhysRevE.87.043112

20. Brujan EA, Ikeda T, Matsumoto Y. Jet formation and shock wave emission during collapse of ultrasound-induced cavitation bubbles and their role in the therapeutic applications of high-intensity focused ultrasound. Phys Med Biol. 2005; 50(20): 4797-4809. doi: 10.1088/0031-9155/50/20/004

21. Iakovlev S, Iakovlev S, Buchner C, et al. Resonance-like phenomena in a submerged cylindrical shell subjected to two consecutive shock waves: The effect of the inner fluid. J Fluids Struct. 2014; 50: 153-170. doi: 10.1016/j.jfluidstructs.2014.05.013

22. Bringa EM, Caro A, Wang YM, et al. Ultrahigh strength in nanocrystalline materials under shock loading. Science. 2005; 309(5742): 1838-1841. doi: 10.1126/science.1116723

23. Kadau K, Germann TC, Lomdahl PS, et al. Shock waves in polycrystalline iron. Phys Rev Lett. 2007; 98(13): 135701. doi: 10.1103/PhysRevLett.98.135701

24. Knudson MD, Desjarlais MP, Dolan DH. Shock-wave exploration of the high-pressure phases of carbon. Science. 2008; 322(5909): 1822-1825. doi: 10.1126/science.1165278

25. Gurnett DA, Kurth WS. Electron plasma oscillations upstream of the solar wind termination shock. Science. 2005; 309(5743): 2025-2027. doi: 10.1126/science.1117425

26. Gurnett DA, Kurth WS. Intense plasma waves at and near the solar wind termination shock. Nature. 2008; 454(7200): 78-80. doi: 10.1038/nature07023

27. Dutton Z, Budde M, Slowe C, Hau LV. Observation of quantum shock waves created with ultra-compressed slow light pulses in a Bose-Einstein condensate. Science. 2001; 293(5530): 663-668. doi: 10.1126/science.1062527

28. Damski B. Shock waves in a one-dimensional Bose gas: From a Bose-Einstein condensate to a Tonks gas. Phys Rev A. 2006; 73(4): 043601. doi: 10.1103/physreva.73.043601

29. Chang JJ, Engels P, Hoefer MA. Formation of dispersive shock waves by merging and splitting Bose-Einstein condensates. Phys Rev Lett. 2008; 101(17): 170404. doi: 10.1103/PhysRevLett.101.170404

30. Millot M, Dubrovinskaia N, Černok A, et al. Planetary science. Shock compression of stishovite and melting of silica at planetary interior conditions. Science. 2015; 347(6220): 418-420. doi: 10.1126/science.1261507

31. McKee CF, Draine BT. Interstellar shock waves. Science. 1991; 252(5004): 397-403. doi: 10.1126/science.252.5004.397

32. McClure S, Dorfmüller C. Extracorporeal shock wave therapy: Theory and equipment. Clin Tech Equine Pract. 2002; 2(4): 348-357. doi: 10.1053/j.ctep.2004.04.008

33. Lingeman JE, McAteer JA, Gnessin E, Evan AP. Shock wave lithotripsy: Advances in technology and technique. Nat Rev Urol. 2009; 6(12): 660-670. doi: 10.1038/nrurol.2009.216

34. Cherenkov PA. Visible emission of clean liquids by action of gamma radiation. R Dokl Akad Nauk SSSR. 1934; 2: 451-454. doi: 10.1234/12345678

35. Rassweiler JJ, Knoll T, Kohrmann KU, et al. Shock wave technology and application: An update. Eur Urol. 2011; 59(5): 784-796. doi: 10.1016/j.eururo.2011.02.033

36. Coleman AJ, Saunders JE. A review of the physical properties and biological effects of the high amplitude acoustic fields used in extracorporeal lithotripsy. Ultrasonics. 1993; 31(2): 75-89. doi: 10.1016/0041-624X(93)90037-Z

37. McAteer JA, Evan AP. The acute and long-term adverse effects of shock wave lithotripsy. Semin Nephrol. 2008; 28(2): 200-213. doi: 10.1016/j.semnephrol.2008.01.003

38. Brümmer F, Bräuner T, Hülser DF. Biological effects of shock waves. World J Urol. 1990; 8(4): 224-232. doi: 10.1007/BF01580025

39. Delius M. Medical applications and bioeffects of extracorporeal shock waves. Shock Waves. 1994; 4(2): 55-72. doi: 10.1007/BF01418569

40. Oosterhof GO, Smits GA, De Ruyter AE, Schalken JA, Debruyne FM. Effects of high-energy shock waves combined with biological response modifiers in different human kidney cancer xenografts. Ultrasound Med Biol. 1991; 17(4): 391-399. doi: 10.1016/0301-5629(91)90139-N

41. Gamarra F, Spelsberg F, Dellian M, Goetz AE. Complete local tumor remission after therapy with extra-corporeally applied high-energy shock waves (HESW). Int J Cancer. 1993; 55(1): 153-156. doi: 10.1002/ijc.2910550127

42. Lauer U, Bürgelt E, Squire Z, et al. Shock wave permeabilization as a new gene transfer method. Gene Ther. 1997; 4(7): 710-715. doi: 10.1038/sj.gt.3300462

43. Bao S, Thrall BD, Gies RA, Miller DL. In vivo transfection of melanoma cells by lithotripter shock waves. Cancer Res. 1998; 58(2): 219-221. Web site. http://cancerres.aacrjournals.org/content/58/2/219.short. Accessed July 24, 2016

44. Delius M, Adams G. Shock wave permeabilization with ribosome inactivating proteins: A new approach to tumor therapy. Cancer Res. 1999; 59(20): 5227-5232. Web site. http://cancerres.aacrjournals.org/content/59/20/5227.long. Accessed July 24, 2016

45. Tschoep K, Hartmann G, Jox R, et al. Shock waves: A novel method for cytoplasmic delivery of antisense oligonucleotides. J Mol Med. 2001; 79(5-6): 306-313. doi: 10.1007/s001090100204

46. Kodama T, Doukas AG, Hamblin MR. Delivery of ribosome-inactivating protein toxin into cancer cells with shock waves. Cancer Lett. 2003; 189(1): 69-75. doi: 10.1016/S0304-3835(02)00503-7

47. Michel MS, Erben P, Trojan L, et al. Acoustic energy: a new transfection method for cancer of the prostate, cancer of the bladder and benign kidney cells. Anticancer Res. 2004; 24(4): 2303-2308. Web site. http://ar.iiarjournals.org/content/24/4/2303.long. Accessed July 24, 2016

48. Ohl C-D, Wolfrum B. Detachment and sonoporation of adherent HeLa-cells by shock wave-induced cavitation. Biochim Biophys Acta. 2003; 1624(1-3): 131-138. doi: 10.1016/j.bbagen.2003.10.005

49. Ohl C-D, Arora M, Ikink R, et al. Sonoporation from jetting cavitation bubbles. Biophys J. 2006; 91(11): 4285-4295. doi: 10.1529/biophysj.105.075366

50. Moosavi-Nejad SF, Hosseini SMR, Satoh M, Takayama K. Shock wave induced cytoskeletal and morphological deformations in a human renal carcinoma cell line. Cancer Sci. 2006; 97(4): 296-304. doi: 10.1111/j.1349-7006.2006.00172.x

51. Bushnell JC, McCloskey DJ. Thermoelastic stress production in solids. J Appl Phys. 1968; 39(12): 5541-5546. doi: 10.1063/1.1656010

52. Yang LC. Stress waves generated in thin metallic films by a Q-switched ruby laser. 1974; 45(6): 2601-2608. doi: 10.1063/1.1663636

53. Fabbro R, Fournier J, Ballard P, Devaux D, Virmont J. Physical study of laser-produced plasma in confined geometry. J Appl Phys. 1990; 68(2): 775-784. doi: 10.1063/1.346783

54. Venugopalan V, Deutsch TF. Stress generated in polyimide by excimer-laser irradiation. J Appl Phys. 1993; 74(6): 4181-4189. doi: 10.1063/1.354422

55. Doukas AG, Flotte TJ. Physical characteristics and biological effects of laser-induced stress waves. Ultrasound Med Biol. 1996; 22(2): 151-164. doi: 10.1016/0301-5629(95)02026-8

56. Yao C-P, Zhang Z-X, Rahmanzadeh R, Huettmann G. Laser-based gene transfection and gene therapy. IEEE Trans Nanobiosci. 2008; 7(2): 111-119. doi: 10.1109/TNB.2008.2000742

57. Doukas AG, Kollias N. Transdermal drug delivery with a pressure wave. Adv Drug Deliver Rev. 2004; 56(5): 559-579. doi: 10.1016/j.addr.2003.10.031

58. Brümmer F, Brenner J, Bräuner T, Hülser DF. Effect of shock waves on suspended and immobilized L1210 cells. Ultrasound Med Biol. 1989; 15(3): 229-239. doi: 10.1016/0301-5629(89)90067-7

59. de Reijke TM, Schamhart DH, Kurth KH, Löwik CW, Donkers LH, Sterenborg HJ. Tumor growth delay by laser-generated shock waves. Lasers Surg Med. 1994; 14(3): 205-212. doi: 10.1002/lsm.1900140302

60. Doukas AG, McAuliffe DJ, Lee S, Venugopalan V, Flotte TJ. Physical factors involved in stress-wave-induced cell injury: The effect of stress gradient. Ultrasound Med Biol. 1995; 21(7): 961-967. doi: 10.1016/0301-5629(95)00027-O

61. Lee S, Anderson T, Zhang H, Flotte TJ, Doukas AG. Alteration of cell membrane by stress waves in vitro. Ultrasound Med Biol. 1996; 22(9): 1285-1293. doi: 10.1016/S0301-5629(96)00149-4

62. Douki T, Lee S, Dorey K, Flotte TJ, Deutsch TF, Doukas AG. Stress-wave-induced injury to retinal pigment epithelium cells in vitro. Lasers Surg Med. 1996; 19(3): 249-259. doi: 10.1002/(SICI)1096-9101(1996)19:3<249::AID-LSM1>3.0.CO;2-S

63. Huber PE, Jenne J, Debus JJ, Wannenmacher MF, Pfisterer P. A comparison of shock wave and sinusoidal-focused ultrasound-induced localized transfection of HeLa cells. Ultrasound Med Biol. 1999; 25(9): 1451-1457. doi: 10.1016/S0301-5629(99)00099-X

64. Kohri K, Uemura T, Iguchi M, Kurita T. Effect of high energy shock waves on tumor cells. Urol Res. 1990; 18(2): 101-105. doi: 10.1007/BF00302468

65. Mulholland SE, Lee S, McAuliffe DJ, Doukas AG. Cell loading with laser-generated stress waves: The role of the stress gradient. Pharm Res. 1999; 16(4): 514-518. doi: 10.1023/A:1018814911497

66. Lee S, Doukas AG. Laser-generated stress waves and their effects on the cell membrane. IEEE J Sel Top Quant. 1999; 5(4): 997-1003. doi: 10.1109/2944.796322

67. Kato M, Ioritani N, Suzuki T, et al. Mechanism of anti-tumor effect of combination of bleomycin and shock waves. Jpn J Cancer Res. 2000; 91(10): 1065-1072. doi: 10.1111/j.1349-7006.2000.tb00886.x

68. Sondén A, Svensson B, Roman N, Brismar B, Palmblad J, Kjellstöm BT. Mechanisms of shock wave induced endothelial cell injury. Lasers Surg Med. 2002; 31(4): 233-241. doi: 10.1002/lsm.10093

69. Kodama T, Kodama T, Hamblin MR, Hamblin MR, Doukas AG. Cytoplasmic molecular delivery with shock waves: Importance of impulse. Biophys J. 2000; 79(4): 1821-1832. doi: 10.1016/S0006-3495(00)76432-0

70. Juhasz T, Hu XH, Turi L, Bor Z. Dynamics of shock waves and cavitation bubbles generated by picosecond laser pulses in corneal tissue and water. Lasers Surg Med. 1993; 15(1): 91-98. doi: 10.1002/lsm.1900150112

71. Strand OT, Goosman DR, Martinez C, Whitworth TL, Kuhlow WW. Compact system for high-speed velocimetry using heterodyne techniques. Rev Sci Instrum. 2006; 77(8): 083108. doi: 10.1063/1.2336749

72. Schmidt M, Kahlert U, Wessolleck J, et al. Characterization of a setup to test the impact of high-amplitude pressure waves on living cells. Nature Sci Rep. 2014; 4: 3849. doi: 10.1038/srep03849

73. Steinhauser MO, Steinhauser MO, Schmidt M. Destruction of cancer cells by laser-induced shock waves: Recent developments in experimental treatments and multiscale computer simulations. Soft Matter. 2014; 10(27): 4778-4788. doi: 10.1039/c4sm00407h

74. Fung YC. Biomechanics: Motion, Flow, Stress, and Growth. New York, USA: Springer; 1990.

75. Verdier C. Rheological Properties of Living Materials. From Cells to Tissues. J Theoretical Medicine. 2003; 5(2): 67-91. doi: 10.1080/10273360410001678083

76. de Gennes PG. Scaling Concepts in Polymer Physics. Ithaca, London, UK; Cornell University Press; 1979.

77. Steinhauser MO. Computational Multiscale Modeling of Fluids and Solids – Theory and Applications. 2^nd ed. New York, USA: Springer; 2016.

78. Steinhauser MO. A molecular dynamics study on universal properties of polymer chains in different solvent qualities. Part I. A review of linear chain properties. J Chem Phys. 2005; 122(9): 094901. doi: 10.1063/1.1846651

79. Bienfait Y. Modelling and molecular dynamics simulations of flexible polymer networks. In: Steinhauser MO, ed. December 2013.

80. Schindler T, Kröner D, Steinhauser MO. On the dynamics of molecular self-assembly and the structural analysis of bilayer membranes using coarse-grained molecular dynamics simulations. Biochim Biophys Acta. 2016; 1858(9): 1955-1963. doi: 10.1016/j.bbamem.2016.05.014

81. Doi M, Edwards SF. The Theory of Polymer Dynamics. New york, USA: Clarendon Press, Oxford; 1986.

82. Bird RB, Hassager O, Armstrong RC, Curtis CF. Dynamics of Polymeric Liquids. New York, USA: Wiley; 1977.

83. Larson RG. The Structure and Rheology of Complex Fluids. New York, USA: Oxford University Press; 1999.

84. Winter HH. Analysis of linear viscoelasticity of a crosslinking polymer at the gel point. J Rheol. 1986; 30(2): 367. doi: 10.1122/1.549853

85. Flory PJ. Statistical Mechanics of Chain Molecules. New Jersey, USA: John Wiley & Sons, Inc; 1969. doi: 10.1002/bip.1969.360080514

86. Einstein A. Eine neue Bestimmung der Moleküldimensionen. Ann Phys. 1906; 324(2): 289-306. doi: 10.1002/andp.19063240204

87. Oldroyd JG. The elastic and viscous properties of emulsions and suspensions. Science. 1953; 218(1132): 122-132. doi: 10.1098/rspa.1953.0092

88. Hashin Z, Rosen BW. The elastic moduli of fiber-reinforced materials. J Appl Mech. 1964; 31(2): 223-232. doi: 10.1115/1.3629590

89. Hill CR. Theory of mechanical properties of fibre-strengthened materials: I. Elastic behaviour. J Mech Phys Solids. 1964; 12(4): 199-212. doi: 10.1016/0022-5096(64)90019-5

90. Fung YC. Microrheology and constitutive equation of soft tissue. Biorheology. 1988; 25(1-2): 261-270. Web site. http://europepmc.org/abstract/med/3196823. Accessed July 24, 2016

91. Choy TC. Effective Medium Theory: Principles and Applications. Oxford, UK: Oxford University Press; 1999. doi: 10.1093/acprof:oso/9780198705093.001.0001

92. Ingber DE, Heidemann SR, Lamoureux P, Buxbaum RE. Opposing views on tensegrity as a structural framework for understanding cell mechanics. J Appl Physiol. 2000; 89(4): 1663-1678. doi: 10.1016/0012-1606(71)90073-X

93. Stamenovic D, Ingber DE. Models of cytoskeletal mechanics of adherent cells. Biomech Model Mechan. 2002; 1(1): 95-108. doi: 10.1007/s10237-002-0009-9

94. Ingber DE. Tensegrity I. Cell structure and hierarchical systems biology. J Cell Sci. 2003; 116(Pt 7): 1157-1173. doi: 10.1242/jcs.00359

95. Wang N, Naruse K, Stamenovic D, et al. Mechanical behavior in living cells consistent with the tensegrity model. Proc Natl Acad Sci. 2001; 98(14): 7765-7770. doi: 10.1073/pnas.141199598

96. Ingber DE, Wang N, Stamenovic D. Tensegrity, cellular biophysics, and the mechanics of living systems. Rep Prog Phys. 2014; 77(4): 046603. doi: 10.1088/0034-4885/77/4/046603

97. Pritchard RH, Huang YYS, Terentjev EM. Mechanics of biological networks: From the cell cytoskeleton to connective tissue. Soft Matter. 2014; 10(12): 1864-1884. doi: 10.1039/c3sm52769g

98. Ingber DE, Madri JA, Jamieson JD. Role of basal lamina in neoplastic disorganization of tissue architecture. PNAS. 1981; 78(6): 3901-3905. Web site. http://www.pnas.org/content/78/6/3901.short. Accessed July 24, 2016

99. Chen D, Wen Q, Janmey PA. Rheology of soft materials. Condensed Matter Physics. 2010; 1: 301-322. doi: 10.1146/annurev-conmatphys-070909-104120

100. Müller KW, Bruinsma RF, Lieleg O, Bausch AR, Wall WA, Levine AJ. Rheology of semiflexible bundle networks with transient linkers. Phys Rev Lett. 2014; 112(23): 238102-238102. doi: 10.1103/PhysRevLett.112.238102

101. Brunner C, Niendorf A, Käs JA. Passive and active single-cell biomechanics: A new perspective in cancer diagnosis. Soft Matter. 2009; 5(11): 2171-2178. doi: 10.1039/b807545j

102. Sayed El T, Mota A, Fraternali F, Ortiz M. A variational constitutive model for soft biological tissues. J Biomech. 2008; 41(7): 1458-1466. doi: 10.1016/j.jbiomech.2008.02.023

103. Qin Z, Dimas L, Adler D, Bratzel G, Buehler MJ. Biological materials by design. J Phys Condens Matter. 2014; 26(7): 073101. doi: 10.1088/0953-8984/26/7/073101

104. Meyers MA, Chen P-Y, Lopez MI, Seki Y, Lin AYM. Biological materials: A materials science approach. J Mech Behav Biomed. 2011; 4(5): 626-657. doi: 10.1016/j.jmbbm.2010.08.005

105. Ogden RW. Large Deformation Isotropic Elasticity – On the Correlation of Theory and Experiment for Incompressible Rubberlike Solids. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 1972; 326(1567): 565-584. doi: 10.1098/rspa.1972.0026

106. Mooney M. A theory of large elastic deformation. J Appl Phys. 1940; 11(9): 582-592. doi: 10.1063/1.1712836

107. Rivlin RS. Large Elastic Deformations of Isotropic Materials. IV. Further Developments of the General Theory. Philosophical Transactions of the Royal Society of London Series A Mathematical and Physical Sciences. 1948; 241(8): 379-397. doi: 10.1098/rsta.1948.0024

108. Miller K, Chinzei K. Mechanical properties of brain tissue in tension. J Biomech. 2002; 35(4): 483-490. doi: 10.1016/S0021-9290(01)00234-2

109. Xu M, Nowinski WL. Talairach-Tournoux brain atlas registration using a metalforming principle-based finite element method. Med Image Anal. 2001; 5(4): 271-279. doi: 10.1016/S1361-8415(01)00045-7

110. Warfield SK, Haker SJ, Talos I-F, et al. Capturing intraoperative deformations: research experience at Brigham and Women’s Hospital. Med Image Anal. 2005; 9(2): 145-162. doi: 10.1016/j.media.2004.11.005

111. Miller K, Chinzei K. Constitutive modelling of brain tissue: Experiment and theory. J Biomech. 1997; 30(11-12): 1115-1121. doi: 10.1016/S0021-9290(97)00092-4

112. Miller K. Method of testing very soft biological tissues in compression. J Biomech. 2005; 38(1): 153-158. doi: 10.1016/j.jbiomech.2004.03.004

113. Wittek A, Kikinis R, Warfield SK, Miller K. Brain shift computation using a fully nonlinear biomechanical model. Med Image Comput Comput Assist Interv. 2005; 8(Pt 2): 583-590. doi: 10.1007/11566489_72

114. Wittek A, Hawkins T, Miller K. On the unimportance of constitutive models in computing brain deformation for image-guided surgery. Biomech Model Mechan. 2008; 8(1): 77-84. doi: 10.1007/s10237-008-0118-1

115. Dumpuri P, Thompson RC, Dawant BM, Cao A, Miga MI. An atlas-based method to compensate for brain shift: Preliminary results. Med Image Anal. 2007; 11(2): 128-145. doi: 10.1016/j.media.2006.11.002

116. Bathe KJ. Finite Element Procedures in Engineering Analysis. Cambridge, UK: Prentice Hall; 1982.

117. Cash DM, Miga MI, Sinha TK, Galloway RL, Chapman WC. Compensating for intraoperative soft-tissue deformations using incomplete surface data and finite elements. IEEE Trans Med Imaging. 2005; 24(11): 1479-1491. doi: 10.1109/TMI.2005.855434

118. Kim JS, Sun SX. Continuum modeling of forces in growing viscoelastic cytoskeletal networks. J Theor Biol. 2009; 256(4): 596-606. doi: 10.1016/j.jtbi.2008.10.023

119. Kim S-H, Suh HS, Cho MH, Lee SY, Kim T-S. Finite element simulation of ultrasound propagation in bone for quantitative ultrasound toward the diagnosis of osteoporosis. Conf Proc IEEE Eng Med Biol Soc. 2009; 2009: 436-439. doi: 10.1109/IEMBS.2009.5334707

120. Hostettler A, George D, Rémond Y, Nicolau SA, Soler L, Marescaux J. Bulk modulus and volume variation measurement of the liver and the kidneys in vivo using abdominal kinetics during free breathing. Comput Meth Prog Bio. 2010; 100(2): 149-157. doi: 10.1016/j.cmpb.2010.03.003

121. Cleveland RO, Lifshitz DA, Connors BA, Evan AP, Willis LR, Crum LA. In vivo pressure measurements of lithotripsy shock waves in pigs. Ultrasound Med Biol. 1998; 24(2): 293-306. doi: 10.1016/S0301-5629(97)00270-6

122. Schwartz J-M, Denninger M, Rancourt D, Moisan C, Laurendeau D. Modelling liver tissue properties using a non-linear visco-elastic model for surgery simulation. Med Image Anal. 2005; 9(2): 103-112. doi: 10.1016/j.media.2004.11.002

123. Nava A, Mazza E, Kleinermann F, Avis NJ, McClure J. Determination of the mechanical properties of soft human tissues through aspiration experiments. Medical Image Computing and Computer-Assisted Intervention. 2003; 2003: 222-229. doi: 10.1007/978-3-540-39899-8_28

124. Ottensmeyer MP. Minimally invasive instrument for in vivo measurement of solid organ mechanical impedance. Web site. https://dspace.mit.edu/handle/1721.1/8858. Accessed July 24, 2016

125. Zhu Y, Dong Z, Wejinya UC, Jin S, Ye K. Determination of mechanical properties of soft tissue scaffolds by atomic force microscopy nanoindentation. J Biomech. 2011; 44(13): 2356-2361. doi: 10.1016/j.jbiomech.2011.07.010